Properties of Liquids - Viscosity
The viscosity of a fluid is that property which tends to resist a shearing force. It can be thought of as the internal friction resulting when one layer of fluid is made to move in relation to another layer.
 Consider the model shown in Fig. 1, which was used by Isaac Newton in first defining viscosity. It shows two parallel planes of fluid of area A separated by a distance dx and moving in the same direction at different velocities V1 and V2.
Consider the model shown in Fig. 1, which was used by Isaac Newton in first defining viscosity. It shows two parallel planes of fluid of area A separated by a distance dx and moving in the same direction at different velocities V1 and V2.
The velocity distribution will be linear over the distance dx, and experiments show that the velocity gradient, dv/dx, is directly proportional to the force per unit area, f/a.
![]() Where n is constant for a given liquid and is called its viscosity.
Where n is constant for a given liquid and is called its viscosity.
The velocity gradient, dv/dx, describes the shearing experience by the intermediate layers as they move with respect to each other. Therefore, it can be called the "rate of shear", S. Also the force per unit area, F/A, can be simplified and called the "shear force" or "shear stress," F. With these simplified terms, viscosity can be defined as follows:
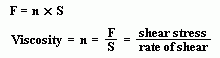
Isaac Newton made the assumption that all materials have, at a given temperature, a viscosity that is independent of the rate of shear. In other words, a force twice as large would be required to move a liquid twice as fast. Fluids which behave this way are called Newtonian fluids. There are, of course, fluids which do not behave this way, in other words their viscosity is dependent on the rate of shear. These are known as Non-Newtonian fluids.
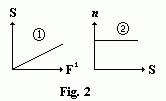
 Fig. 2 shows graphically the relationships between shear stress (F,)rate of shear (S,) and viscosity (n) for a Newtonian liquid. The viscosity remains constant as shown in sketch 2, and in absolute units, the viscosity is the inverse slope of the line in sketch 1. Water and light oils are good examples of Newtonian liquids.
Fig. 2 shows graphically the relationships between shear stress (F,)rate of shear (S,) and viscosity (n) for a Newtonian liquid. The viscosity remains constant as shown in sketch 2, and in absolute units, the viscosity is the inverse slope of the line in sketch 1. Water and light oils are good examples of Newtonian liquids.
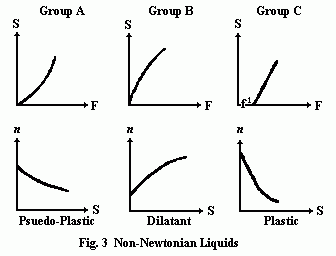 Fig. 3 shows graphically the three most common types of Non-Newtonian liquids. Group A shows a decreasing viscosity with an increasing rate of shear. This is known as pseudo-plastic material. Examples of this type are grease, molasses, paint, soap, starch, and most emulsions. They present no serious pumping problems since they tend to thin out with the high rates of shear present in a pump.
Fig. 3 shows graphically the three most common types of Non-Newtonian liquids. Group A shows a decreasing viscosity with an increasing rate of shear. This is known as pseudo-plastic material. Examples of this type are grease, molasses, paint, soap, starch, and most emulsions. They present no serious pumping problems since they tend to thin out with the high rates of shear present in a pump.
Group B shows a dilatant material or one in which the viscosity increases with an increasing rate of shear. Clay slurries and candy compounds are examples of dilatant liquids. Pumps must be selected with extreme care since these liquids can become almost solid if the shear rate is high enough. The normal procedure would be to oversize the pump somewhat and open up the internal clearances in an effort to reduce the shear rate.
Group C shows a plastic material. The viscosity decreases with increasing rate of shear. However, a certain force must be applied before any movement is produced. This force is called the yield value of the material. Tomato catsup is a good example of this type of material. It behaves similar to a pseudo-plastic material from a pumping standpoint.
The viscosity of some Non-Netonian liquids is dependent upon time as well as shear rate. In other words, the viscosity at any particular time depends upon the amount of previous agitation or shearing of the liquid. A liquid whose viscosity decreases with time at a given shear rate is called a thixotropic liquid. Examples are asphalts, glues, molasses, paint, soap, starch, and grease. Liquids whose viscosity increases with time are called rheopectic liquids, but they are seldom encountered in pumping applications.
There are two basic viscosity parameters: Dynamic (or absolute) viscosity and kinematic viscosity. Dynamic viscosities are given in terms of force required to move a unit area a unit distance. This is usually expressed in pound-seconds per square foot in the English system which is equal to slugs per foot-second. The Metric system is more commonly used, however, in which the unit is the dyne-second per square centimeter called the Poise. This is numerically equal to the gram per centimeter-second. For convenience, numerical values are normally expressed in centipoise, which are equal to one-hundredth of a poise.
Most pipe friction charts and pump correction charts list kinematic viscosity. The basic unit of kinematic viscosity is the stoke which is equal to a square centimeter per second in the Metric system. The corresponding English unit is square foot per second. The centistoke which is on-hundredth of a stoke is normally used in the charts. The following formula is used to obtain the kinematic viscosity when the dynamic or absolute viscosity is known:
![]()
There are numerous type of viscometers available for determining liquid viscosities, most of which are designed for specific liquids or viscosity ranges. The Saybolt viscometers are probably the most widely used in the United States. The Saybolt Universal Viscometer measures low to medium viscosity, and the Saybolt Furol Viscometer measures high viscosities. The corresponding units are the SSU (Seconds Saybolt Universal) and the SSF (Seconds Saybolt Furol.) These units are found on most pipe friction and pump correction charts in addition to centistokes. A conversion chart for these and other units is shown in the next section of this manual.
Viscosity Correction Centrifugal Pumps
A general rule of thumb - The performance of a centrifugal pump must be corrected if the viscosity of the liquid exceeds 30 cps. Refer to the manufacturers performance conversion data.